terça-feira, 21 de outubro de 2008
Pega Matemático!
Ao morrer um pai deixou 90 000 reais aos filhos. São nove homens e cada um deles tem uma irmã. Sabendo-se que a divisão será feita em partes iguais, quanto receberá cada um? Digite a resposta dispondo os algarismos de acordo com os exemplos a seguir: 1 500, 30 000 ou 550 000.
segunda-feira, 20 de outubro de 2008
Regra de três e fraçao!
Carla e sua mãe fazem crochê muito bem e resolveram tecer uma colcha juntas. Sabendo que Carla teceria a colcha sozinha em 30 dias e sua mãe, também sozinha, em 20 dias, em quantos dias as duas juntas concluiriam o serviço?
Acontece que após 5 dias de trabalho, das duas juntas, a mãe de Carla precisou viajar e pediu à filha que concluíse o trabalho. Contando, a partir do dia 1º, em que dia o trabalho foi concluído?
Acontece que após 5 dias de trabalho, das duas juntas, a mãe de Carla precisou viajar e pediu à filha que concluíse o trabalho. Contando, a partir do dia 1º, em que dia o trabalho foi concluído?
Probleminha de 5ª Série (FRAÇÃO)
Uma torneira enche um tanque em 4 horas e, se este tanque estiver cheio, a quantidade de água que escoa pelo ralo o deixa vazio em 5 horas. Se a torneira estiver aberta, mas a água, ao mesmo tempo, saindo pelo ralo, o tanque ficará cheio? Por que? Quanto tempo leverá para encher o tanque?
Será que todo mundo encontrou 20 horas.
Veja porque:
um quarto de um quinto é igual a um vinte avos
1/4 x 1/5 = 1/20
para tornar o tanque com fração inteira ficaria 20/20 portanto em 20 horas o tanque encheria.
Próxima semana outra explicação para o mesmo problema!
Será que todo mundo encontrou 20 horas.
Veja porque:
um quarto de um quinto é igual a um vinte avos
1/4 x 1/5 = 1/20
para tornar o tanque com fração inteira ficaria 20/20 portanto em 20 horas o tanque encheria.
Próxima semana outra explicação para o mesmo problema!
quinta-feira, 21 de agosto de 2008
Planificação geométrica
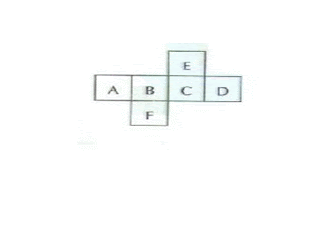
Na figura acima, temos a planificação de um cubo:
Imagine que o cubo tenha sido montado.
Nesse caso, a face oposta à face B é a face:
a) A
b) C
c) D
d) F
Esta é fácil. Chama-se planificação de figuras geométricas e uma ótima abstração. A resposta certa é a letra c o "D" está atrás do "B" quando você fechar o cubo
sexta-feira, 4 de julho de 2008
Probabilidade!!!!!!
Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a probabilidade de sair uma bola azul. (Lembre-se probabilidade é dada em porcentagem.)
Respota:
Resolução:
a. sair bola azul P(A)=6/20=3/10=0,30=30% "
b. sair bola vermelha P(A)=10/20=1/2=0,50= 50% "
c. sair bola amarela P(A) = 4/20=1/5 =0,2 =20% "
Respota:
Resolução:
a. sair bola azul P(A)=6/20=3/10=0,30=30% "
b. sair bola vermelha P(A)=10/20=1/2=0,50= 50% "
c. sair bola amarela P(A) = 4/20=1/5 =0,2 =20% "
Essa é fácil - Equação do 2º Grau
Um número somado com o seu quadrado é igual a 90. Que números são esses?
Essa é só aplicar a fórmula de Báskara.
x+x²=90
transformando
x²+x-90=0
delta
1²-4.1.(-90)
1+360
361
x=-1+ou-19 (raiz de 361)/2
x' = -1+19/2 = 18/2 = 9
x"= -1-19/2=-20/2 = -10
Portanto os números são
9 e -10
Essa é só aplicar a fórmula de Báskara.
x+x²=90
transformando
x²+x-90=0
delta
1²-4.1.(-90)
1+360
361
x=-1+ou-19 (raiz de 361)/2
x' = -1+19/2 = 18/2 = 9
x"= -1-19/2=-20/2 = -10
Portanto os números são
9 e -10
quinta-feira, 29 de maio de 2008
Lembra disso..................... Função composta!!!!
Fabiano, a fim de reduzir o preço da conta de telefone de sua casa, decidiu fazer um relatório geral, catalogando a quantidade de ligações feitas por dia juntamente com as suas respectivas tarifas. Nas suas anotações, ele constatou que cada pessoa faz, em média, 4 ligações por dia e também que cada ligação custa mais ou menos R$ 0,70. Com intuito de ajudar Fabiano, vamos analisar matematicamente essa situação:
Se Fabiano não quiser que o valor da sua conta de telefone mensal seja maior que R$ 168, 00, quantas pessoas no máximo deverão utilizar o telefone diariamente?
Resolução:
y = 4x
z = 0,70y
Substituindo 4x no lugar de y na função z:
z = 0,70.4x
z = 2,8x
Se Fabiano não quiser que o valor da sua conta de telefone mensal seja maior que R$ 168, 00, quantas pessoas no máximo deverão utilizar o telefone diariamente?
z = 2,8x
168 = 2,8x
x = 60
60 pessoas durante o mês.
Adotando que o mês tem 30 dias, podemos concluir que o máximo de pessoas que devem utilizar o telefone diariamente, para que não ultrapasse o valor estabelecido por Fabiano, são duas pessoas.
Resposta: 2 pessoas
Com os conceitos apresentados, dadas duas funções reais: f(x) = 2x – 1 e g(x) = x + 2, podemos calcular a função composta de g e f, expressa pela notação (g o f) (x), que é equivalente à g (f(x)). Para isso, devemos substituir no lugar de x na função g a lei de função f.
g(x) = x + 2
g(f(x)) = g(2x – 1) = 2x – 1 + 2 = 2x +1
g(f(x)) ou (g o f) (x) = 2x +1
De modo análogo, podemos calcular a função composta de f em g, substituindo no lugar de x na função f a lei de função g:
f(x) = 2x - 1
f(g(x)) = f(x + 2) = 2.(x + 2) – 1 = 2x + 4 – 1 = 2x + 3
f(g(x)) ou (f o g) (x) = 2x + 3
Praticando...
1) Sendo f(x) = x +2 e f(g(x)) = 5x -1, determine g(x).
f(x) = x + 2
f(g(x)) = g(x) + 2 = 5x – 1
g(x) = 5x – 1 – 2
g(x) = 5x -3
2) Sendo g(x) = x + 1 e f(g(x)) = 4x -5, determine f(x).
g(x) = z
x +1 = z
x = z – 1
f(z) = 4.(z – 1) - 5
f(z) = 4z – 4 – 5
f(z) = 4z – 9 = f(x) = 4x - 9
Se Fabiano não quiser que o valor da sua conta de telefone mensal seja maior que R$ 168, 00, quantas pessoas no máximo deverão utilizar o telefone diariamente?
Resolução:
y = 4x
z = 0,70y
Substituindo 4x no lugar de y na função z:
z = 0,70.4x
z = 2,8x
Se Fabiano não quiser que o valor da sua conta de telefone mensal seja maior que R$ 168, 00, quantas pessoas no máximo deverão utilizar o telefone diariamente?
z = 2,8x
168 = 2,8x
x = 60
60 pessoas durante o mês.
Adotando que o mês tem 30 dias, podemos concluir que o máximo de pessoas que devem utilizar o telefone diariamente, para que não ultrapasse o valor estabelecido por Fabiano, são duas pessoas.
Resposta: 2 pessoas
Com os conceitos apresentados, dadas duas funções reais: f(x) = 2x – 1 e g(x) = x + 2, podemos calcular a função composta de g e f, expressa pela notação (g o f) (x), que é equivalente à g (f(x)). Para isso, devemos substituir no lugar de x na função g a lei de função f.
g(x) = x + 2
g(f(x)) = g(2x – 1) = 2x – 1 + 2 = 2x +1
g(f(x)) ou (g o f) (x) = 2x +1
De modo análogo, podemos calcular a função composta de f em g, substituindo no lugar de x na função f a lei de função g:
f(x) = 2x - 1
f(g(x)) = f(x + 2) = 2.(x + 2) – 1 = 2x + 4 – 1 = 2x + 3
f(g(x)) ou (f o g) (x) = 2x + 3
Praticando...
1) Sendo f(x) = x +2 e f(g(x)) = 5x -1, determine g(x).
f(x) = x + 2
f(g(x)) = g(x) + 2 = 5x – 1
g(x) = 5x – 1 – 2
g(x) = 5x -3
2) Sendo g(x) = x + 1 e f(g(x)) = 4x -5, determine f(x).
g(x) = z
x +1 = z
x = z – 1
f(z) = 4.(z – 1) - 5
f(z) = 4z – 4 – 5
f(z) = 4z – 9 = f(x) = 4x - 9
sexta-feira, 23 de maio de 2008
Palitinho... esse é meu forte!
Uma criança está brincando de fazer quadrados com palitos de fósforos como mostra o desenho a seguir.
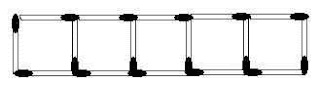
a) Quantos palitos são necessários para fazer 100 quadrados?
b) Quantos quadrados ela fez com 250 palitos?
Para facilitar: essa é uma PA com razão 3
a) Para fazer um quadrado é necessário 4 palitos. Para fazer dois quadrados é necessário 7 palitos. Para fazer três quadrados é necessário 10 palitos , e assim por diante. Então, temos uma progressão aritmética: PA (4 , 7 , 10 , 13 , 16 , ... ), onde o primeiro termo a1 = 4, a razão r = 3 . Assim, temos que encontrar o centésimo termo a100 = a1 + 99r = 4 + 99(3) = 4 + 297 = 301 .
b) O enésimo termo an = a1 + (n-1)r é o número de palitos e o número de termos n é o número de quadrados . Assim, 250 = a1 + (n-1)r. Segue que 250 = 4 + (n - 1)(3). O que implica em, 250 = 4 + 3n - 3. Daí, vem que:: n = (250 - 1) / 3. Logo: n = 249 / 3 = 83 quadrados.

a) Quantos palitos são necessários para fazer 100 quadrados?
b) Quantos quadrados ela fez com 250 palitos?
Para facilitar: essa é uma PA com razão 3
a) Para fazer um quadrado é necessário 4 palitos. Para fazer dois quadrados é necessário 7 palitos. Para fazer três quadrados é necessário 10 palitos , e assim por diante. Então, temos uma progressão aritmética: PA (4 , 7 , 10 , 13 , 16 , ... ), onde o primeiro termo a1 = 4, a razão r = 3 . Assim, temos que encontrar o centésimo termo a100 = a1 + 99r = 4 + 99(3) = 4 + 297 = 301 .
b) O enésimo termo an = a1 + (n-1)r é o número de palitos e o número de termos n é o número de quadrados . Assim, 250 = a1 + (n-1)r. Segue que 250 = 4 + (n - 1)(3). O que implica em, 250 = 4 + 3n - 3. Daí, vem que:: n = (250 - 1) / 3. Logo: n = 249 / 3 = 83 quadrados.
terça-feira, 20 de maio de 2008
Futebol e Matemática!!!!!
Se num campeonato de futebol é verdade que “quem não faz, leva”, ou seja, time que não marca gol numa partida sofre ao menos um gol nessa mesma partida, então:
a) em todos os jogos os dois times marcam gols
b) nenhum jogo termina empatado
c) o vencedor sempre faz um gol a mais que o vencido
d) nenhum jogo termina 0 x 0, ou seja, sem gols
e) resultados como 1 x 0, 2 x 0 ou 3 x 0 não são possíveis
Essa foi muito fácil - Letra certa d - alguém vai ter que marcar, pois quem não faz, leva, ou ele ganha ou ele perde. Isso só acontece na Matemática.
a) em todos os jogos os dois times marcam gols
b) nenhum jogo termina empatado
c) o vencedor sempre faz um gol a mais que o vencido
d) nenhum jogo termina 0 x 0, ou seja, sem gols
e) resultados como 1 x 0, 2 x 0 ou 3 x 0 não são possíveis
Essa foi muito fácil - Letra certa d - alguém vai ter que marcar, pois quem não faz, leva, ou ele ganha ou ele perde. Isso só acontece na Matemática.
sábado, 10 de maio de 2008
Probleminha simples de 6ª série...
A mãe pede ao filho Antoninho:
- Filho vai no Empório ( nome de casas comerciais) do seu Joaquim e compra manteiga.
O filho bem depressa vai ao Empório. Chegando lá ele pede ao seu Joaquim.
- Seu Joaquim, seu Joaquim eu quero manteiga. O Senhor tem aí?
- Tenho sim Antoninho, responde o seu Joaquim, mas só tenho 1 milésimo de tonelada.
- Ah seu Joaquim, mas eu só quero 1 hectograma da manteiga.
Pergunta:
Quanto de manteiga tem o Seu Joaquim pra vender?
Quanto de manteiga comprou o Antoninho?
Fácil , fácil!!!!!!
Fácil Mesmo!!!!!!!!!!!!!!!!!!
O seu joaquim tem 1kg de manteiga - 1 milésimo da tonelada 1.000kg dividido por mil.
O Antoninho 100 g de manteiga.
- Filho vai no Empório ( nome de casas comerciais) do seu Joaquim e compra manteiga.
O filho bem depressa vai ao Empório. Chegando lá ele pede ao seu Joaquim.
- Seu Joaquim, seu Joaquim eu quero manteiga. O Senhor tem aí?
- Tenho sim Antoninho, responde o seu Joaquim, mas só tenho 1 milésimo de tonelada.
- Ah seu Joaquim, mas eu só quero 1 hectograma da manteiga.
Pergunta:
Quanto de manteiga tem o Seu Joaquim pra vender?
Quanto de manteiga comprou o Antoninho?
Fácil , fácil!!!!!!
Fácil Mesmo!!!!!!!!!!!!!!!!!!
O seu joaquim tem 1kg de manteiga - 1 milésimo da tonelada 1.000kg dividido por mil.
O Antoninho 100 g de manteiga.
terça-feira, 6 de maio de 2008
Divisão é fácil; o difícil é problema com divisão....
Numa divisão entre numeros naturais, o quociente é o igual ao divisor, e o resto é o maior possivel. Se o resto for igual a 11, qual será o dividendo ?
Resposta:
Como o resto é 11 e ele é o maior possível, assim o divisor só pode ser 12 e o quociente também. Então fica assim: 12 x 12 = 144 + 11 (que é o resto) = 155 é o dividendo.
Um abraço!!!!
sexta-feira, 2 de maio de 2008
Problema......Conjunto ( Use o diagrama de Venn)
(PUC) Um levantamento sócio-econômico entre os habitantes de uma cidade revelou que, exatamente: 17% têm casa própia; 22% têm automóvel; 8% têm casa própria e automóvel. Qual o percentual dos que não têm casa própria nem automóvel?
Diagrama de Venn - 1ª dica
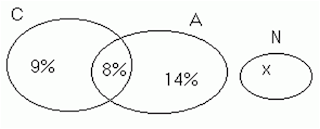
E agora ficou fácil ???????
Pois bem esta é a resposta..... 9+ 8 + 14 = 31 faltando para 100%, 69%.
Então 69% não tem casa própria nem automóvel.
Diagrama de Venn - 1ª dica

E agora ficou fácil ???????
Pois bem esta é a resposta..... 9+ 8 + 14 = 31 faltando para 100%, 69%.
Então 69% não tem casa própria nem automóvel.
A Matemática Lander
A partir de hoje você entrará em contato com a matemática. Terá ótimas oportunidades de resolver alguns problemas simples, apenas para fazer uma abstração e desenvolver os raciocínios mais simples da matemática.
Um abraço cartesiano a todos.
Marcos Lander
Um abraço cartesiano a todos.
Marcos Lander
Assinar:
Comentários (Atom)
Frases Famosas
- Se A é o sucesso, então A é igual a X mais Y mais Z. O trabalho é X; Y é o lazer; e Z é manter a boca fechada.
