Problema desafio!

6 pessoas se encontram e uma cumprimenta a outra com um aperto de mão.  Quantos apertos de mãos aconteceram neste encontro?

Etnomatemática

A ETNOMATEMÁTICA E SUAS POSSIBILIDADES PEDAGÓGICAS: ALGUMAS INDICAÇÕES1

Benerval Pinheiro Santos2

A etnomatemática na sala de aula: concepções iniciais

É natural aceitar que, a princípio, a etnomatemática esteve relacionada com a matemática de grupos culturais bem definidos – povos indígenas; povos africanos; povos antigos; entre outros. Contudo, pautados nos congressos nacionais e internacionais da área3 e, bem como, nos trabalhos de alguns dos seus estudiosos, é possível reconhecer uma constante preocupação com as implicações pedagógicas da etnomatemática (KNIJNIK, 1996; D’AMBROSIO, 1993, 1998, 2001; FERREIRA, 1997; VERGANI, 2000; GERDES, 1991).

Entretanto, qual é a verdadeira função do programa etnomatemático enquanto interveniente nos sistemas formais de ensino? Quais são suas verdadeiras possibilidades? Como explorá-las e implementá-las? São questões que ainda merecem certo destaque. Pois, mesmo reconhecendo a etnomatemática como “um programa de pesquisas em história e filosofia da matemática, com óbvias implicações pedagógicas” (D’AMBROSIO, 2001a, p. 27), poucas indicações práticas têm sido feitas em relação ao seu encaminhamento pedagógico e, adicionalmente a esse quadro, os entendimentos acerca da questão não são compartilhados do mesmo modo.

Em verdade, não somos defensores da necessidade de um consenso entre os entendimentos sobre as perspectivas da etnomatemática como interveniente nas práticas pedagógicas. Ao contrário, consideramos a diversidade de opiniões como uma característica enriquecedora do processo educativo em transformação. Porém, podemos reconhecer que a diversidade de opiniões em relação à questão deriva do atual estágio de desenvolvimento em que essa área se encontra.

Como exemplo da compreensão e aplicação das contribuições da etnomatemática em sala de aula, tomemos dois trabalhos apresentados no Primeiro Congresso Internacional de Etnomatemática – I CIEm, que são bem contemplativos. O primeiro é de autoria de Luis ORTIZ‑FRANCO (1998), com o sugestivo título: “Ethnomathematics in Classroom”. Em sua comunicação, ele mostrou “(...) como podemos usar o sistema numérico dos Astecas Mexicanos no ensino das propriedades comutativas, associativas e distributivas da álgebra e, assim, integrarmos sistemas não decimais no ensino de matemática” (p.1).

De modo algum discordamos do valor histórico do sistema numérico dos Astecas ou o de qualquer outro povo. Porém, fazer a utilização sugerida pelo autor, de forma sistematizada, com o intuito de facilitar algo que não necessariamente está inserido num contexto mais amplo ou leva em conta interesses do grupo, pode ser entendido como um reducionismo. Esse trabalho, de certa forma, ainda centra a questão do ensino como sendo o ponto fulcral e utiliza uma matemática, alheia ao grupo de alunos, como um ente facilitador/motivador, ou ainda, como uma curiosidade que tem a função de facilitar o ensino da matemática tradicional. De algum modo, esse trabalho parece encontrar respaldo ou, ainda, tangenciar a visão de GERDES (1991, p. 5), quando este afirma que “estudos etnomatemáticos analisam tradições matemáticas que sobreviveram à colonização e actividades matemáticas na vida diária das populações, procurando possibilidades de as incorporar no currículo”. Entretanto Gerdes, ao fazer tal afirmação, está falando das “tradições matemáticas” das populações às quais o ensino está direcionado e não de tradições e populações distintas.

O segundo trabalho que também nos serve de exemplo é de autoria de Holly L. WENGER (1998), intitulado “Examples and Results of Teaching Middle School Mathematics from an Ethnomathematical Perspective”, cujas considerações na perspectiva do ensino são assim defendidas:

Ensinar sob uma perspectiva etnomatemática é um modo de promover reformas no ensino, engajando os estudantes na descoberta da matemática de seus cotidianos, de seus pais e amigos de muitas culturas. A perspectiva etnomatemática traz interesse, excitação e relatividade para os estudantes, que serão mais motivados como estudantes de matemática em geral.

Nesse trabalho, podemos perceber um traço marcante em comparação com o primeiro – o ensino de matemática deixa de ser o único foco da aula, ele preocupa-se também com a aprendizagem, no sentido de que os conteúdos passam a ser significativos para os educandos, porque estes é que são colocados no centro do processo educativo e não os conteúdos. Percebemos também, no trabalho de WENGER, grande preocupação com a motivação dos alunos para aprender “a matemática em geral”. Nesse sentido, podemos relacionar a visão da autora à de FERREIRA (1997).

FERREIRA (1997) defende a Etnomatemática como uma “Proposta Pedagógica”, “Modelo Pedagógico” ou ainda, “um método de se ensinar matemática” (p. 16). Em seu trabalho o autor defende/propõe as técnicas da etnografia para o trabalho de campo com os educandos. Ou seja, os alunos sairiam a campo, como fazem os pesquisadores acadêmicos, principalmente antropólogos e, por meio de entrevistas, gravações, notas, estudariam a matemática do grupo ou um problema da comunidade, uma curiosidade/questão proposta pelos alunos, entre outros.

Grosso modo, o que o autor propõe está muito próximo do que propõem os modeladores matemáticos, ou seja, a modelagem matemática. Em suma, o roteiro é de alguma forma muito parecido ao roteiro utilizado pelos modeladores.

Pode ser que a idéia do “Modelo Pedagógico” de FERREIRA tangenciar a modelagem matemática, talvez seja uma conseqüência da concepção inicial da etnomatemática, isto é, como sendo a matemática de grupos culturais em particular (BARTON, 1995, p. 206) e, desse modo, cabendo aos pesquisadores e pesquisadoras descobrir essa matemática, utilizando as técnicas da modelagem matemática. Essa concepção de FERREIRA pode ser também percebida em MONTEIRO (1998, p. 14), quando esta afirma: “Abordo também a Modelagem Matemática como uma ferramenta do processo da Etnomatemática, numa abordagem pedagógica”.

É possível notarmos, nos trabalhos na linha indicada por FERREIRA, tentativas que vão na direção do quadro mais ou menos esboçado por VIEIRA (1999, p. 132) quando afirma:

A matemática escrita apresenta inúmeras vantagens do ponto de vista do desenvolvimento do aluno que aqui não cabe agora explicitar. Quero sim frisar quão importante considero os professores conhecerem, reconhecerem, entenderem e valorizarem a matemática oral, o que implica aprenderem a fazer antropologia do quotidiano dos seus alunos [grifo nosso].

Depois, a resolução de problemas na sala de aula é sem dúvida uma forma privilegiada de estabelecer essa tão querida ligação entre a matemática e a vida, a abstração e o dia a dia. Trata-se, em face da multiculturalidade – a heterogeneidade cultural –, construir a interculturalidade, a coexistência da diversidade na unidade.

Assim, para alguns pesquisadores, ir a campo com os alunos para pesquisar manifestações matemáticas da comunidade seria um encaminhamento pedagógico da etnomatemática. Isso pode ser percebido em vários trabalhos. Entre eles estão os de BORBA (1987), de FERREIRA (1997), de MONTEIRO (1998), de WENGER (1998).

De todo modo, vale enfatizar, os trabalhos mencionados são preciosos por levantarem questões centrais comuns aos trabalhos da etnomatemática vista como proposta pedagógica. No de ORTIZ-FRANCO, fica implícita a idéia de que o conteúdo matemático deve ser ensinado e que os problemas do ensino de matemática podem ser enfrentados contextualizando-se os conteúdos da matemática acadêmica com exemplos de matemáticas de outras culturas. E, no de WENGER, é levantada uma questão prática muito próxima à do primeiro, entretanto considerando, talvez como elemento de motivação, a matemática do grupo social composto pelos alunos, seus pais, mães e amigos.

Desses trabalhos surgem questões de algum modo norteadoras, tais como: o ensino, numa perspectiva etnomatemática, tem como preocupação apenas a motivação para a aprendizagem da matemática tradicional, utilizando matemáticas (etnomatemáticas) de outras culturas? Ou ainda, a etnomatemática tem como preocupação a substituição dos conteúdos da matemática formal pelos da matemática do grupo social? É parte intrínseca da etnomatemática a modelagem matemática de problemas que emergem do mundo real, como sugere FERREIRA (1997)? E, novamente, quais são as preocupações de uma proposta para a educação matemática na perspectiva da etnomatemática?

Partiremos, assim, para uma discussão que tentará se não responder, pelo menos clarear um pouco as questões acima.

É objetivo da etnomatemática substituir a matemática acadêmica?

Naturalmente, é de grande valia para a pedagogia4 etnomatemática, procurar saber qual é o conhecimento etnomatemático do grupo, pois esse conhecimento tem valor cultural e afetivo. Porém, cabe nos questionarmos sobre que ganhos a comunidade teria se substituísse os conhecimentos matemáticos formais instituídos pelos seus conhecimentos etnomatemáticos. Pois, o grupo social está, de fato, inserido em um meio sociocultural mais abrangente – em um país – com valores, condutas e mecanismos5 próprios que delimitam o acesso e/ou a ascensão de seus membros às diversas escalas sociais e carreiras profissionais.

Assim, os conhecimentos etnomatemáticos, sob esse ponto de vista utilitário, teriam pouca ou nenhuma utilidade, pois não são reconhecidos como válidos6 pela sociedade.

Por isso, vemos como equivocada a idéia de substituir a matemática acadêmica pela etnomatemática. Entretanto, mesmo a etnomatemática tendo utilidade limitada na sociedade moderna, igualmente, muito da matemática acadêmica é absolutamente inútil nessa sociedade (D’AMBROSIO, 2001, p. 43), justificando-se a permanência de muito do que a compõe apenas pelos mecanismos ressaltados acima.

Entretanto, por um lado, consideramos que “A disciplina denominada matemática é uma etnomatemática que se originou e se desenvolveu na Europa, tendo recebido algumas contribuições das civilizações indianas e islâmicas” (Ibidem, p. 73). Logo, não deveria ter maior valor em relação aos conhecimentos etnomatemáticos de certos grupos no seio da sociedade. Por outro lado, quando afirmamos que ao processo pedagógico da matemática não cabe substituir os conteúdos da matemática acadêmica, da mesma forma defendemos que é sua tarefa relevar a etnomatemática da comunidade. Está aqui, portanto, estabelecido o conflito – o convívio com a dúvida.

De todo modo, o que a princípio parece ser contraditório, pode ser resolvido frente à “contextualização”7 (Ibidem, pp. 76-77). Entretanto, “Stephen Smale, nos lembra que há termos de matemática que, embora corretos e interessantes, não são importantes. Igualmente, o ensino da matemática corre o risco de se ater a conteúdos sem importância, isto é, inúteis” (Ibidem, p. 14).

Dessa forma, mesmo reconhecendo que muitos conteúdos hoje são obsoletos, colocamos como questão o envolvimento efetivo/reflexivo dos educadores sobre o processo ensino-aprendizagem. Ou seja, como mencionamos, não vemos a substituição pura e simples de conteúdos como algo que resolveria o problema do ensino e aprendizagem da matemática. Ainda, a sua eliminação dos programas poderia representar nenhum avanço ao ensino tradicional de matemática. Da mesma forma, podemos reconhecer, vai na mesma direção a inclusão de novos conteúdos. Isso porque “a fraqueza do ensino não está no conteúdo, mas na forma como se ensina” (ITURRA, 1994, p. 46).

Ainda nesse sentido, parece haver uma certa confusão em relação ao valor da matemática como instrumento utilitário em nossa sociedade. De alguma forma, o silêncio de muitos frente à manutenção desse ensino arcaico e conservador de matemática, reforça a idéia de que todos os conteúdos são úteis e por isso merecem ser ensinados. Sobre isso, cabe aqui ressaltar que a distância entre a defesa de certos conteúdos pelo seu valor utilitário não está muito distante da defesa de sua utilização, ingenuamente ou conscientemente, como um instrumento de perpetuação do status quo e, conseqüentemente, como um instrumento de seleção social, filtro social. Porém, “as conseqüências da ingenuidade e da perversidade não são essencialmente diferentes” (D’AMBROSIO, 2001, p. 80) quando observamos os resultados desse ensino. De qualquer forma, defender o primeiro – seu valor utilitário – mesmo não implicando aceitar o segundo – como instrumento de seleção – deve ser visto com certa cautela.

Em relação a essa questão, KNIJNIK (1996, p. 89) apresenta importante subsídio para nossa análise, ao afirmar:

Os grupos socialmente subordinados (....) expressam sua necessidade de dominar a Matemática acadêmica frente aos desafios cotidianos que têm no confronto com a lógica e os processos que constituem e são constituídos pelos saberes oficiais dos grupos dominantes.

E, em concordância com o que defendemos, continua sua argumentação, afirmando que:

Não se trata, portanto, de glorificar a Matemática popular, celebrando-a em conferências internacionais, como uma preciosidade a ser preservada a qualquer custo. Este tipo de operação não empresta nenhuma ajuda aos grupos subordinados. Enquanto intelectuais, precisamos estar atentas/os para não pô-la em execução, exclusivamente na busca de ganhos simbólicos no campo científico ao qual pertencemos. No entanto, não se trata de negar à matemática popular sua dimensão de autonomia, tão cara às teorias relativistas. (Ibidem, p. 89)

É nesse panorama que assentamos nossa crença na contextualização, nos moldes delineados por Ubiratan D’Ambrosio, como um importante subsídio à pedagogia etnomatemática. Fato esse que não nega, apenas engloba, os avanços proporcionados pelos autores e autoras mencionados.

Com efeito, colocamos como inerente à etnomatemática, com inclinações pedagógicas, relevar os conhecimentos próprios do grupo escolar. Porém, de certa forma, apenas deslocamos as questões mencionadas para a questão: como contextualizar e promover o diálogo, entre a matemática e a etnomatemática em situação de ensino e aprendizagem nos sistemas formais de ensino?

Assim, naturalmente faremos uso de outros paradigmas educacionais na tentativa de responder à questão.

Pedagogia etnomatemática: educação intercultural e libertadora

De forma natural, a pedagogia etnomatemática encontra subsídio também na antropologia sem, contudo, trazer para si a pretensão de inclusão nessa área. Nesse sentido, frente aos trabalhos mencionados, é possível afirmar que a educação etnomatemática prima pelo reconhecimento do outro.

Estamos assim perante a questão de como lidar com diferentes culturas, do problema da comunicação entre diferentes (...) Quer dizer, compreender o outro não é só falar a sua língua para o ouvir e perceber, mas é também conhecer a sua cultura, ou melhor a sua mente cultural, o seu contexto, a sua mentalidade (...).

(VIEIRA, 1995, p. 133)

Então, nesse diálogo entre diferentes, reivindica o seu lugar no programa pedagógico etnomatemático, também, o conceito/paradigma da pedagogia intercultural (ITURRA, 1995; VIEIRA, 1995, 1999; D’AMBROSIO, 2001). Pedagogia essa que tem por lugar comum a realidade multicultural das sociedades, pleiteando um processo pedagógico centrado não só no ensino, mas também na aprendizagem, buscando a comunicação e a troca entre os diferentes, pondo em pé de igualdade as vias de acessos sociais, mas “sem perder a identidade local” (VIEIRA, 1995, p. 134). De alguma forma colocando-se

Contra uma educação meramente multicultural, que respeita as diferenças culturais e mentalidades mas que as deixa navegar em artérias paralelas, ou avenidas de pouca liberdade (...), contra também as políticas de unificação, assimilação e adesão a uma única cultura hegemônica, a pedagogia intercultural situar-se-ia, ou situar-se-á (... não em ideologias, mas sim na possibilidade de realizar o que falta fazer) numa perspectiva dinâmica e interacionista de enriquecimento e de aprendizagem pela troca de saberes, pelo diálogo de culturas.

(VIEIRA, 1995, p. 142-143)

Na direção de uma pedagogia intercultural, D’AMBROSIO (2001, p. 61) afirma que: “Na educação, estamos vendo um crescente reconhecimento da importância das relações interculturais. Mas lamentavelmente, ainda há relutância no reconhecimento das relações interculturais”.

A “relutância” mencionada pelo autor, de alguma maneira, encontra reforço nas atuais formas de organização curricular, impondo um currículo único, por exemplo, às mesmas séries sem relevar as características próprias do público educando. Também, as formas de avaliação impositivas e padronizadas, a insistência em se organizar as séries por aproveitamentos nesses testes, são efetivamente tentativas de pasteurizar as novas gerações (D’AMBROSIO, 2001, p. 61).

Assim, na forma de intervenção, o modelo intercultural implica uma dialética em constante contradição, assegurando a diferença sem contudo a sustentar. Desse modo, o interculturalismo implica reconhecer as diferenças e, também, fazer com que sejam origem de inovações e situações de enriquecimento recíprocos pela troca (VIEIRA, 1995, p. 143).

Na mesma direção, tem lugar na pedagogia etnomatemática, a pedagogia libertadora de FREIRE, ao trazer para si a tarefa de atuar contra os mecanismos de reprodução instituídos, para “desvendar a realidade que está sendo ocultada pela ideologia dominante, pelo currículo dominante” (FREIRE & SHOR, 2000, p. 49).

E assim, alinhada à “pedagogia intercultural” de VIEIRA, ITURRA e D’AMBROSIO, e à “pedagogia libertadora” de FREIRE, centramos a pedagogia etnomatemática de D’AMBROSIO.

Entretanto, frente a esses modelos, ou paradigmas educacionais, coloca-se naturalmente a própria realidade da escola, assim como, de toda a nossa sociedade, com seus vícios e ranços como obstáculos a serem superados. Mais precisamente, reconhecemos que a dinâmica histórica, na qual se alicerça nossa escola, seja o maior obstáculo, pois “sabemos que não é a educação que modela a sociedade, mas, ao contrário, a sociedade é que modela a educação segundo os interesses de quem detém o poder” (FREIRE & SHOR, 2000, p. 49). Dessa forma, “a mudança a operar passa por uma transformação qualitativa da educação, pela construção de uma sociedade de aprendizagem, e particularmente por uma educação permanente que abranja não só as excepções, mas todos os cidadãos e a sociedade no seu conjunto” (VIEIRA, 1995, p. 140).

E como operacionalizar essa mudança? Naturalmente, a resposta não é direta nem imediata, mas certamente a figura do professor surge como ponto central nesse processo. Pois, decididamente, não vemos como possível operar mudanças profundas e inclusivas por decreto, sem uma mudança qualitativa nas concepções dos professores e das professoras, assim como dos educandos.

Indicação de caminhos

Nas diversas instâncias de troca entre educadoras e educadores matemáticos – congressos, seminários e colóquios da área – é comum surgirem questões do tipo: “Qual seria o método da etnomatemática em sala de aula?”; ou, “Como se ensina sob a perspectiva da etnomatemática?”. Em geral, por um lado, tal preocupação dos professores e professoras pode ser uma conseqüência natural da forma tradicional do processo educativo ser tão somente de ensino, como mencionamos. Outro fator, talvez, venha do professor ver-se etnocêntrico, visão promovida pela e na escola.

Por outro lado, no dia-a-dia das salas de aula, os educadores são cobrados de diversas formas, ou ainda, são confrontados com uma realidade inadequada ao desenvolvimento de atividades que confluam em direção ao respeito à diversidade cultural ou sociocultural e à aprendizagem.

Assim, a preocupação por ter algo pronto, na qualidade de uma técnica ou um método, que possa aplicar de forma imediata tornou-se, de algum modo, inerente ao ato de ensinar nos moldes tradicionais.

Entretanto, defendemos a etnomatemática não como um método de ensino em si, mas sim como detentora de relações inclusivas entre professores e alunos e das diversas formas de conhecer presentes em contextos culturais/socioculturais diferentes. Isso porque, mais importante que a mudança/indicação de métodos e técnicas, é a necessidade de haver/desenvolver questionamentos e reflexões sobre as nossas próprias práticas, condutas e idéias (VIEIRA, 1999).

Contudo, mesmo não tendo por objetivo atrelar à etnomatemática um método ou técnica de ensino específicos, indicaremos, a seguir, a nossa concepção de possíveis encaminhamentos dessa pedagogia em sala de aula.

Porém, antes, tomaremos emprestado de ITURRA (1994) e VIEIRA (1995; 1999), o “método comparativo”; de D’AMBROSIO (2001), a contextualização; e, de FREIRE (1996, 2000), “o método dialógico”, para assentarmos nossas concepções sobre possíveis encaminhamentos da pedagogia etnomatemática.

Fortemente influenciado por ITURRA, na direção do “modelo intercultural” de educação, VIEIRA (1995, p. 143-144) argumenta que:

A metodologia é através da comparação e da contextualização – o método comparativo – entre os diferentes mundos e contextos sócio-culturais (Cf. Abdallah-Preceill: 1986 e Iturra, 1990). É que sem comparar não se apreende, não se assimila, eventualmente memoriza-se e papagueia-se. É por isso que não há normas universais para ensinar nem uma única forma de aprender. É preciso conhecer culturalmente o destinatário para que o ensino produza de facto aprendizagem.

Nesse sentido, a comparação entra na pedagogia etnomatemática, por um lado, como um instrumento de auto regulação das próprias atividades de ensino/aprendizagem, pois na medida em que o professor busca constantemente compreender para além das circunstâncias imediatas de seu meio social, acaba por empreender uma constante busca por novas maneiras e alternativas de ensino – e o que é necessário ser ensinado/aprendido. E por outro lado, nessa dinâmica, será natural comparar-se com o outro que faz diferente, implicando conhecer a si próprio, tomando consciência de suas próprias representações, do seu modo próprio de fazer.

Dessa maneira, a comparação funciona também como um instrumento a ser desenvolvido e utilizado pelo aluno em sua construção pessoal e social, pois:

(...) a comparação em si mesma, acaba por ser um processo comum ao pensamento humano (...) Ninguém se pensa no abstracto. Comparamo-nos com os outros. Os outros nos dão a imagem daquilo que somos, daquilo que queremos ou mesmo daquilo que não queremos. Tudo isso implica um método comparativo na construção identitária do self. O próprio eu constrói-se comparando o seu ontem com o seu hoje, por forma a posicionar-se no futuro – a construção do projecto pessoal.

(VIEIRA, 1999, p. 137)

Nessa direção, tomando consciência de si e dos outros à sua volta, tanto os professores quanto os alunos, através da comparação, terão à frente a questão do contexto a ser enfrentada e superada. E nesse processo, a questão relacionada a que matemática ensinar, fica razoavelmente relativisada. Ou seja, pretender que uma – a matemática acadêmica – seja mais eficiente, mais rigorosa, enfim, melhor que a outra – a etnomatemática do grupo/comunidade –, é uma questão que, se removida do contexto, é falsa e falsificadora. É fato que o conhecimento etnomatemático do grupo/comunidade tem certamente muito valor, pois lhe serve, é eficiente e adequada para muitas coisas, próprias àquela cultura, àquele etno, e não há por que substituí-la. Da mesma forma, a matemática do grupo dominante lhe serve, é útil e não há como ignorá-la (D’AMBROSIO, 2001, p. 80-81).

Desse modo, quando lançamos mão do método comparativo, da contextualização e do método dialógico, para assentarmos a pedagogia etnomatemática, enfatizamos que essa pedagogia relaciona-se a uma postura crítica por parte tanto do educador quanto do educando com o conhecimento. Dito de outro modo,

A utilização do cotidiano das compras para ensinar matemática revela práticas apreendidas fora do ambiente escolar, uma verdadeira etnomatemática do comércio. Um importante componente da etnomatemática é possibilitar uma visão crítica da realidade, utilizando instrumentos de natureza matemática.

(D’AMBROSIO, 2001, p. 23)

Ou seja, nessa relação/educação dialógica, vale enfatizar, os conteúdos tradicionais terão importância secundária, isto é, estarão a serviço, de certo modo, do desvelar da realidade para o desenvolvimento dos educandos e educandas. Dessa forma, serão relevantes os conteúdos que, de algum modo, apresentarem subsídio à intenção de desvelar a realidade, isto é, que sejam conteúdos críticos, sejam eles parte da matemática acadêmica ou da etnomatemática da comunidade.

Em outras palavras, “A matemática contextualizada se mostra como mais um recurso para solucionar problemas novos” (D’AMBROSIO, 2001, p. 80). Problemas estes que, de certo modo estão relacionados, por vezes, a princípios básicos da matemática, normalmente aceitos sem contestação, devido à idéia muito difundida de sua suposta neutralidade e universalidade. Um exemplo disso pode ser tomado nas operações aritméticas. Na operação de adição, por exemplo, GADOTTI (1991, p. 43), argumenta que:

Uma coisa é a soma do ponto de vista capitalista, e outra é o significado da soma para o trabalhador. O capitalista, na sua soma, inclui uma parte do trabalho assalariado. Na soma do assalariado, esse só pode contar consigo mesmo e com seus companheiros de trabalho. Até a matemática, que parece tão neutra, pode ser contextualizada.

E, do mesmo modo, sob um aspecto mais amplo, a contextualização reivindica o seu lugar nas relações de ensino e aprendizagem na pedagogia etnomatemática, pois:

Afinal, como deixar de relacionar os Elementos de Euclides com o panorama cultural da Grécia Antiga? Ou a adoção da numeração indo-arábica na Europa com o florescimento do mercantilismo nos séculos XIV e XV? E não se pode entender Newton descontextualizado? (...) Alguns dirão que a contextualização não é importante, que o importante é reconhecer a matemática como a manifestação mais nobre do pensamento e da inteligência humana... e assim justificam sua importância nos currículos.

(D’AMBROSIO, 2001, p. 76-77)

E, dessa forma, o dilema excluir/incluir conteúdos fica de algum modo superado. A contextualização suprime essa falsa questão, colocando no centro das atenções as questões maiores, relacionadas à aprendizagem, inclusão social...

Assim, entre esse processo dinâmico de comparar e contextualizar tem lugar o “método dialógico” de FREIRE. Nesse contexto, vale ressaltar que:

(...) deveríamos entender o ‘diálogo’ não como uma técnica apenas que podemos usar para conseguir obter alguns resultados. Também não podemos, não devemos, entender o diálogo como uma tática que usamos para fazer dos alunos nossos amigos. Isso faria do diálogo uma técnica para a manipulação, em vez de iluminação. Ao contrário, o diálogo deve ser entendido como algo que faz parte da própria natureza histórica dos seres humanos. (...) Isto é, o diálogo é uma espécie de postura necessária, na medida em que os seres humanos se transformam cada vez mais em seres criticamente comunicativos. O diálogo é o momento em que os humanos se encontram para refletir sobre sua realidade tal como a fazem e re-fazem. (...) Através do diálogo, refletindo juntos sobre o que sabemos e não sabemos podemos, a seguir, atuar criticamente para transformar a realidade.

(...) O diálogo sela o relacionamento entre os sujeitos cognitivos, podemos, a seguir, atuar para transformar a realidade.

(FREIRE & SHOR, 2000, p. 122-123)

E na mesma direção, SHOR, argumenta que: “O diálogo libertador é uma comunicação democrática, que invalida a dominação e reduz a obscuridade, ao afirmar a liberdade dos participantes de refazer sua cultura” (FREIRE & SHOR, 2000, p. 123).

Ainda, “o diálogo é este encontro dos homens, mediatizados pelo mundo, para pronunciá-lo, não se esgotando, portanto, na relação eu-tu” (FREIRE, 2000, p. 78);

Dessa forma, entendemos o “diálogo”, a “contextualização” e a “comparação”, como pilares que alicerçam a pedagogia etnomatemática podendo, ainda, ser entendidos como posturas necessárias ao professor dentro dessa pedagogia.

Paulo Freire e a Pedagogia etnomatemática.

Ainda, vemos de forma natural a pedagogia etnomatemática sedimentando-se enquanto prática e buscando forte subsídio no denominado método Paulo Freire8. Ela empresta desse método as suas premissas básicas. Sendo a principal delas a busca pelo entendimento da realidade do sujeito no sentido de buscar subsídio para emprestar aos sujeitos, educandos e educandas, ferramentas para que possam compreender a realidade que os envolve e para modificá-la, dentro de seus anseios políticos e socioculturais.

Desse modo, o casamento entre a pedagogia etnomatemática e o método Paulo Freire é, em essência, natural, quando olhamos mais de perto os seus encaminhamentos. O segundo não se limita a alfabetizar os educandos, como mencionamos, mas também desenvolver neles e com eles a consciência crítica. Da mesma forma, a primeira não se limita a ensinar matemática aos educandos e educandas, mas sim, de alguma forma, tendo como norte as diversas etnomatemáticas, almeja alfabetizá-los matematicamente relevando suas formas matemáticas próprias, suas realidades e anseios, seus meios socioculturais e culturais...

Contudo, essa dinâmica, como defendido até aqui, não pode ser feita de forma alienígena ao sujeito educando, mas com ele. Pois, a superação de idéias não se faz no ato de consumi-las, mas no de produzi-las e de transformá-las na ação e na comunicação. E nesse processo, se o pensar do educando é ingênuo, será pensado o seu pensar, na ação, que ele mesmo se superará (FREIRE, 2000, p. 101).

Dessa forma, a pedagogia etnomatemática, que tem como um dos seus objetivos a busca do pensar do povo, não pode ser feita de forma alheada de uma prática problematizadora. Ou seja, a pedagogia etnomatemática alinha-se à pedagogia de Paulo Freire, também, na medida em que carrega atrelada a si uma prática problematizadora, sob a qual “vão os educandos desenvolvendo o seu poder de captação e de compreensão do mundo que lhes aparece, em suas relações com ele. Não mais como uma realidade estática” (Ibidem, p. 71).

Nesse sentido, reconhecemos na pedagogia etnomatemática as mesmas etapas do método de Paulo Freire. Sendo essas etapas esquematizadas em três momentos: da investigação; da tematização; da problematização (GADOTTI, 1991, p. 39-40; FREIRE, 2000).

Dentro do ambiente formal de ensino e aprendizagem de matemática, a primeira etapa, a da investigação, pode ser encaminhada na forma de uma mesa redonda com os educandos, com o objetivo de deixar mais ou menos claras as concepções do processo educativo da matemática, do professor e dos educandos. Consideramos importante essa etapa pois, de certo modo e com poucas variações, os alunos vêm de um ensino tradicional, com forte influência tecnicista. Assim, um confronto, primeiramente no nível das concepções, é necessário. Porém, esse confronto, naturalmente, deverá ser feito de forma inclusiva, convidando os alunos a terem voz em um espaço que normalmente nunca tiveram – na aula de matemática. E esse fato causa, é possível supor, um certo choque nos alunos.

Ainda nessa primeira etapa, o educador deverá estar atento para o universo do aluno, para as falas que, de alguma forma, denunciem a realidade que o envolve.

Já na segunda etapa – a da tematização – o professor ouve os alunos para descobrir temas que deverão ser organizados como problemas, desafiando a percepção prévia que os alunos têm da realidade e do assunto em questão. .

Nesse sentido,

Freire é igualmente insistente em que seu conceito de educação dialógica não significa que os professores sejam meramente presenças passivas, acidentais (1992) (...) Os professores podem ser fortes influências, sem serem superiores, que controlam totalmente o ambiente de aprendizagem.

(FRANKENSTEIN, s/d, p. 116).

Entretanto, o tema não deve ser visto como uma hipótese de trabalho que deva ser comprovada. Se assim o fosse, a investigação não seria em torno dele, mas de sua existência ou não (FREIRE, 2000, p. 88).9

Na terceira etapa, a da problematização, as situações de aprendizagem e de ensino passarão a centrar-se, também, nas atividades. Mas devem ser considerados tanto conteúdos quanto métodos. Pois, um conteúdo emancipador se apresentado numa forma não libertadora reduzirá insights críticos e não desafiará a realidade tomada-por-certa pelos educandos (FRANKENSTEIN, s/d, p. 111-112).

Vale ressaltar, é nessa direção de encaminhamentos que, de algum modo, poderão emergir dos alunos suas maneiras próprias de quantificar, de inferir, de resolver problemas, de entender a sua realidade, a sua matemática, isto é, a sua etnomatemática.

Entretanto, esse fato, ou seja, o reconhecimento na fala dos alunos de uma certa etnomatemática, deve sim ser comemorado, mas não como se o educador houvesse atingido um fim ou os objetivos da pedagogia etnomatemática. Porque, o emergir, nas falas dos alunos, de conhecimentos próprios, representa um indício, ou ainda, um dos objetivos da rotina da aula dialógica, da pedagogia etnomatemática, não um fim...

De algum modo a pedagogia etnomatemática, como mencionamos, não poderia ter como objetivo simplesmente o reconhecimento da etnomatemática do grupo, pois isso, mediante o que já expusemos, não representaria ganho algum, se isento de um contexto, de uma causa maior, isto é, do que consideramos como apreensão da realidade e de uma aprendizagem, por parte do sujeito educando.

---

1 O presente artigo, essencialmente, foi baseado em nossa pesquisa de mestrado – SANTOS (2002) - defendida em novembro de 2002, na Faculdade de Educação da Universidade de São Paulo.

2 Mestre e Doutorando em Educação Matemática pela FE/USP. Professor Assistente do Centro Universitário São Camilo. Membro do GEPEm (FE/USP).

bene@fe.usp.br

3 O Primeiro Congresso Internacional de Etnomatemática – I CIEm, ocorreu em Granada em 1998; o II CIEm, em Ouro Preto, em 2002; e o Primeiro Congresso Brasileiro de Etnomatemática – CBEm 1, ocorreu em São Paulo em 2000 e o CBEm 2 está programado para ocorrer em abril/2004 na cidade de Natal.

4 A palavra pedagogia está sendo usada aqui não como relativa a uma teoria e ciência do ensino, mas como relativa ao ato/ofício de ensinar. Caso prefira, pode trocá-la por abordagem ou proposta. Contudo, não usamos esses termos por entendermos que eles dizem menos que o pretendido no contexto do trabalho. Dessa forma, indicaremos em itálico a palavra pedagogia quando estivermos nos referindo ao ofício de ensinar/aprender pautado na etnomatemática.

5 Por mecanismos de acesso, podemos entender, algo torpe como vestibulares, avaliações nacionais ou outras formas de acessos profissionais, como concursos públicos e privados.

6 A título de exemplo, podemos citar o caso dos pedreiros que, notoriamente, têm formas próprias de quantificar/inferir e medir úteis em suas atividades, mas que não são reconhecidas – validadas - pelos sistemas formais de transmissão de conhecimento e não são contempladas pelos mecanismos que mencionamos.

7 Vale enfatizar que não estamos utilizando o termo contextualizar num de seus significados mais superficiais comumente utilizado, o de dar exemplos e aplicações do tópico matemático que se está ensinando, mas, sim, num sentido amplo de buscar os encadeamentos lógicos, formais, históricos, políticos e quotidianos do assunto matemático tratado e colocá-los a serviço do desenvolvimento intelectual, afetivo, político e cultural do aluno e não a serviço da própria matemática, como normalmente tem acontecido.

8 Quando falamos em método Paulo Freire estamos, de alguma forma, fazendo uso de um chavão muito difundido, não só no Brasil, a respeito das teorizações de Paulo Freire na direção da alfabetização primordialmente de adultos, desenvolvidas por ele no início da década de 60 e difundidas em diversos países e povos como um método de alfabetização. Entretanto, como ressalta GADOTTI (1991, p. 32): “A rigor não se poderia falar em 'método' Paulo Freire pois se trata muito mais de uma teoria do conhecimento e de uma filosofia da educação do que de um método de ensino”.

9 Em nossa pesquisa de mestrado (SANTOS, 2002), apresentamos o seguinte exemplo de tema: após as discussões e diálogos, entre a professora e seus educandos de 5ª série, surgiram dúvidas sobre o que seria medida. Então, o tema medida foi colocado e, como problematizadora e direcionadora das atividades, a professora apresentou a questão: o que é medir? E quase todas as atividades e situações de aprendizagem durante boa parte do ano letivo giraram em torno dela.

A desvalorização do profissional da educação em Minas Gerais

Professor: desvalorização e extinção!

Nos mais remotos tempos, da época da Grécia Antiga e de Roma, os Sábios eram proclamados os professores dos filhos dos reis e detinham todos os privilégios da nobreza. Numa época mais próxima toda família tinha orgulho em ter entre ela um parente próximo quer era professor. Na zona rural, as moças eram preparadas para serem a “professorinha” da localidade. E hoje como somos?

Atualmente pode-se dizer que passa muito, mas muito longe esse privilégio ou honra de ser professor, pois as escolas estão sucateadas, sem qualquer tecnologia para acompanhar a evolução dos tempos e a superdesvalorização do profissional em educação. Essa desvalorização que passa através de um salário básico que não chega perto do Salário Mínimo (acredite!), sendo que um profissional em final de carreira que ganha um salário de R$ 2.000,00 (dois mil reais) com toda as vantagens (biênios, qüinqüênios, etc) pode dar graças a Deus porque está recebendo bem demais, até porque os profissionais em educação quem entram hoje para dar aula no Estado não tem direito mais de obter esta vantagens, ou seja, biênio e qüinqüênios e outras vantagens foram abolidas do plano de cargos e salários do profissional de educação.

Hoje a proliferação de faculdades e universidades particulares que formam os professores com aulas semi-presenciais (final de semana) ou até mesmo pela internet não são poucas e isto influencia diretamente na qualidade do profissional que está sendo formado. Não bastasse isso temos os cursos de pós-graduação que nem precisam da presença física deste profissional, basta apenas enviar o pagamento das mensalidades e para desespero de nossa classe e da qualidade educacional qualquer outra profissão (engenheiro, médico, psicólogo, segundo grau completo, etc) pode dar aula basta concorrer e não ter o profissional específico para aquela matéria.

E neste ponto que o sistema educacional começa a ruir. Podemos chegar a uma defasagem de milhões e milhões de professores faltando em nosso País. Salários injustos, desvalorização profissional e sucateamento fazem com que estes profissionais procurem outras formações ou larguem sua profissão por outra que não tenha tanto desgaste e que receba tão pouco. E olha que professores da matéria de Física, Química e Biologia já são peças raríssimas de serem encontrados.

As escolas além de ensinar têm que substituir muitas vezes os pais das crianças que ali freqüentam sobrecarregando ainda mais esta função. Para se ter uma idéia um professor com 36 aulas semanais tem que cumprir mais 4 horas por semana de reuniões e aulas de reforço, cumprir 200 dias letivos de aula, uma semana de férias em julho, IPSEMG (nosso INSS) falido sem médicos para atender, sem estrutura física (sem carteiras, cadeiras e nem se fala em note book com data-show). A que ponto chegamos? Quem vai querer ser PROFESSOR? E quando faltar o que a sociedade vai fazer pra suprir esta falta?

“Acho que vivi em época errada queria ser o Sábio do reino que tinha os privilégios e não ser considerado um peso salarial para o Estado”

Malba Tahan.......

O PROBLEMA DAS OITO CAIXAS - Malba Tahan

Segundo uma lenda muito antiga, o célebre Califa Al Motacém Billah, rei dos árabes, chamou certa manhã o astucioso Sabag, seu vizir-tesoureiro, e disse-lhe em tom grave, como se ditasse uma sentença irrevogável:
— Dentro de poucas horas, meu caro vizir, receberei a visita do jovem Beremisz Samir, apelidado “o homem que calculava”. Não ignoras, certamente, que o talentoso Beremiz tem deslumbrado esta nossa gloriosa Bagdá com inequívocas demonstrações de seu incomparável engenho e de sua agudíssima inteligência. Os enigmas mais intrincados, os cálculos mais difíceis são, pelo exímio matemático, explicados e resolvidos em rápidos momentos. É meu desejo presentear o ilustre Beremiz com avultada quantia. Gostaria, entretanto, de experimentar também a tão elogiada argúcia do calculista, propondo-lhe durante a nossa entrevista um problema que seja relacionado, de certo modo, com o prêmio que lhe darei em moedas de ouro. Um problema que deixasse o nosso visitante encantado, é verdade, mas também perplexo e confuso.
O vizir Sabag não era homem que se deixasse entibiar diante dos caprichos e fantasias do poderoso emir. Depois de ouvir, cabisbaixo e pensativo, as palavras do rei, ergueu o rosto bronzeado, fitou serenamente o glorioso califa, e assim falou:
— Escuto e obedeço, ó Príncipe dos Crentes! Pelo tom de vossas palavras, adivinho perfeitamente o rumo seguido pela caravana de vossas intenções. É vosso desejo premiar um sábio geômetra com valiosa quantia. Ressalta, dessa intenção, a generosidade sem par de vosso coração. Quereis, entretanto, que este prêmio seja exornado com um problema original e inédito, capaz de surpreender o mais engenhoso dos matemáticos e de encantar o mais delicado dos filósofos. Essa lembrança põe em relevo a elegância de vossas atitudes, pois o visitante, ao ser argüído diante da corte, poderá mais uma vez demonstrar a pujança de seu engenho e o poderio de sua cultura.
Proferidas tais palavras, retirou-se o vizir para a sua sala de trabalho. Decorrido algum tempo, voltou à presença do rei, precedido de dois escravos núbios que conduziam pesada bandeja de prata. Repousavam sobre a bandeja oito caixas de madeira, todas do mesmo tamanho, numeradas de um até oito.
Não pequeno foi o espanto do califa de Bagdá ao ver aquele singular aparato. Qual seria a razão de ser daquelas caixas numeradas de um até oito? Que mistério, no domínio das contas e dos cálculos, poderiam elas envolver? Cheiques e nobres, que se achavam ao lado do rei, entreolhavam-se espantados.
Cabia ao honrado Sabag, ministro da corte, explicar o porquê daquela estranha preparação. Ouçamos, pois, o relato feito pelo digno vizir:
— Cada uma dessas caixas contém um certo número de moedas. O total contido nas caixas é o prêmio que será oferecido ao calculista. As caixas, como podeis observar, estão numeradas de um até oito, e dispostas segundo o número de moedas que cada uma contém. Para esse arranjo das caixas, adotei a ordem crescente. Assim, a caixa designada pelo número 1 encerra o menor número de moedas; vem depois a que é indicada pelo número 2; a seguir aparece a de número 3, e assim por diante até a última, que encerra o maior número de moedas. Para evitar qualquer dúvida, direi desde logo que não é possível encontrar duas caixas com o mesmo número de moedas.
O califa, seriamente intrigado, interpelou o vizir:
— Não percebo, ó eloqüente Sabag, que problema seria possível formular com esses dinares distribuídos por oito caixinhas. Por Allah! Não percebo!
O vizir Sabag, quando moço, fora professor primário e havia aprendido, diante das classes, a ensinar os iletrados, a esclarecer as dúvidas dos menos atilados e dirimir as questões sugeridas pelos mais espertos. Firmemente resolvido a elucidar o glorioso soberano, o velho mestre-escola assim falou:
— Cumpre-me dizer, ó Rei do Tempo, que os dinares não foram distribuídos ao acaso pelas oito caixas. Cada caixa encerra um certo número de moedas. São ao todo, portanto, oito quantias em dinares. Com as quantias distribuídas pelas oito caixas, podemos fazer qualquer pagamento, desde um dinar até o número total contido nas oito caixas, sem precisar abrir nenhuma caixa ou tocar em moeda alguma. Basta separar, da coleção que se acha sobre a bandeja, uma, duas, três, quatro ou mais caixas, e será obtido o total desejado.
— Iallah! É curioso! — comentou maravilhado o emir. — Segundo posso inferir de tua explicação, o arranjo dos dinares, distribuídos pelas oito caixas, permite que se possa retirar do total a quantia que se quiser, sem violar nenhuma das caixas, sem remover moeda alguma?
— Isso mesmo! — confirmou pressuroso o vizir. — Digamos que fosse vosso desejo retirar, por exemplo, do total a quantia de 212 dinares. Nada mais simples. No grupo das oito caixas há algumas cujas porções nelas contidas perfazem a soma de 212. Consistirá a dificuldade do problema, para cada caso, em determinar as caixas que devem ser separadas, a fim de que se obtenha uma determinada quantia, pois o que se fez para 212 poder-se-á fazer para 200, 49, 157, ou qualquer número inteiro até o total de moedas.
Feita breve pausa, a fim de permitir que o rei pudesse fixar idéias e refletir sobre o caso, o inteligente vizir rematou:
— Eis, ó Comendador dos Crentes, em resumo, o problema que poderia ser proposto, diante da corte, ao genial calculista: “Sabendo que estas caixas, numeradas de um até oito, contêm dinares em números que não se repetem; sabendo-se também que é possível efetuar qualquer pagamento até o número total de moedas, sem abrir nenhuma caixa, pergunta-se:
1º - Quantas moedas contém, respectivamente, cada uma das caixas?
2º - Como determinar, por meio do raciocínio, matematicamente certo, a quantia contida em cada uma?
3º - Qual o número total de moedas?
4º - Será possível resolver o mesmo problema distribuindo-se as moedas por um número menor de caixas?”
O divã do califado, isto é, o salão real das audiências, achava-se repleto de nobres e convidados quando, pelo soar surdo e solene do gongo, foi anunciada a visita de Beremiz Samir, “o homem que calculava”. No centro do suntuoso recinto, sobre luxuoso tapete, foi colocada a bandeja com as oito caixas que iriam servir de base para o problema.
Al-Motacém Billah, Príncipe dos Crentes, que se achava em seu trono de ouro e púrpura, rodeado de seus vizires e cádis, dirigiu ao matemático amistosa saudação:
— Sê bem-vindo, ó Beremiz! Sê bem-vindo sob a inspiração de Allah! Que a tua presença neste divã seja motivo de júbilo para todos os nossos amigos, e que de tuas palavras possamos colher as tâmaras deliciosas da sabedoria que eleva as almas e purifica os corações.
Decorreu um momento de impressionante silêncio. Competia ao visitante agradecer aquela honrosa saudação. Inclinando-se Beremiz diante do rei, assim falou:
— Allah badique, ia Sidi! — Deus vos conduza, ó Chefe! Admiro, estimo e exalto aqueles que governam com justiça, bondade e sabedoria. É esse o vosso caso, ó Emir dos Árabes, e todos os vossos súditos proclamam essa verdade. A vossa justiça assegura o poderio do Estado; a vossa bondade cria preciosas dedicações; e a vossa sabedoria fortalece e perpetua a confiança do povo. Ai daqueles cujos governantes são sábios mas regem a vida pela injustiça das ações que praticam! Ai daqueles cujos chefes e dirigentes são justos mas desconhecem a bondade! E Allah, o Clemente, se compadeça daqueles que se acham sob o jugo de homens ignorantes, pérfidos e iníquos.
— As tuas palavras, ó calculista — respondeu o rei mansamente — são para mim como brincos de ouro e rubis. Servem-me de estímulo e enchem-me de orgulho. Vou, mais uma vez, abusar de tua gentileza. Será um encanto, não só para mim, como para todos os nobres, vizires e cheiques que aqui se acham, ouvir a tua palavra, a tua doutíssima opinião, sempre original e brilhante, sobre um problema aritmético que parece desafiar o engenho dos mais insignes matemáticos. Esse problema, formulado pelo vizir Sabag, poderia ser enunciado nos seguintes termos: “Sobre aquela bandeja estão oito caixas. Cada caixa contém um certo número de moedas, e não há duas caixas com o mesmo número de moedas. Afirma o vizir Sabag que a distribuição de moedas pelas oito caixas foi feita de modo a permitir que se possa, do total, destacar qualquer quantia, desde um dinar, sem abrir nenhuma caixa, isto é, sem tocar nas moedas. Resta agora determinar quantas moedas contém cada caixa e qual o total de moedas. Para facilitar a exposição, as caixas estão numeradas de um até oito, segundo a ordem crescente das quantias que encerram”.
E o califa rematou, depois de breve pausa:
— Como orientarias, ó calculista, a solução desse engenhoso problema?
Beremiz Samir, “o homem que calculava”, como bom súdito, não se fez de rogado. Cruzou lentamente os braços, baixou o rosto e pôs-se a meditar. Depois de coordenar as idéias, iniciou a preleção sobre o caso, nos seguintes termos:
— Em nome de Allah, Clemente e Misericordioso! Esse problema é, realmente, um dos mais interessantes que tenho ouvido, e a sua solução, por ser simples e suave, põe em relevo a beleza e a simplicidade sem par da Matemática. Vejamos. A distribuição dos dinares pelas oito caixas foi feita de modo a permitir que separemos uma quantia qualquer, a partir de um dinar, destacando-se da coleção uma, duas, três ou mais caixas. Resta determinar o conteúdo de cada caixa. É evidente que a primeira caixa deve conter um dinar, pois do contrário não poderíamos destacar a unidade do total. Eis a conclusão algemada pela evidência: a caixa designada pelo número 1 contém um dinar.
A segunda caixa deverá conter, forçosamente, dois dinares, pois a quantia de um dinar não pode ser repetida, e se a segunda caixa tivesse três, quatro ou mais dinares não seria possível separar dois dinares do total. Conclusão: já conhecemos os conteúdos respectivos das duas primeiras caixas. Com auxílio dessas duas caixas podemos obter um, dois ou três dinares.
Passemos agora à terceira caixa. Quanto deveria conter? A resposta impõe-se imediatamente: quatro dinares. Com efeito, se a terceira caixa encerrasse mais de quatro dinares, não seria possível, conservando intactas as caixas, separar quatro dinares do total. Para as três primeiras, temos, portanto:
1ª caixa: 1 dinar;
2ª caixa: 2 dinares;
3ª caixa: 4 dinares.
Com auxílio dessas três caixas, podemos formar todas as quantias desde um até sete dinares. Sete representaria o total das três primeiras caixas, isto é, um mais dois mais quatro.
Repetindo o mesmo raciocínio, somos levados a afirmar que a caixa seguinte, isto é, a quarta, deverá conter oito dinares. A inclusão desta caixa com oito dinares permitirá separar do total todas as quantias desde um até quinze. O quinze é formado pelo conteúdo das quatro primeiras caixas.
E a quinta caixa? Não oferece o cálculo de seu conteúdo a menor dificuldade. Uma vez demonstrado que as quatro primeiras caixas totalizam quinze, é evidente que a quinta caixa deverá encerrar dezesseis dinares. A inclusão da quinta caixa ao grupo das quatro primeiras permite que formemos qualquer número desde um até trinta e um, inclusive. O total trinta e um é obtido pela soma das cinco primeiras.
Neste ponto fez o calculista uma pausa rapidíssima, e logo prosseguiu:
— Vejamos, pelo encadeamento natural de nosso raciocínio, se é possível descobrir uma lei, ou regra, que permita calcular os conteúdos respectivos das outras caixas restantes. Para isso convém recapitular:
1ª caixa: 1 moeda;
2ª caixa: 2 moedas;
3ª caixa: 4 moedas;
4ª caixa: 8 moedas;
5ª caixa: 16 moedas.
Observemos que cada caixa, a partir da segunda, contém sempre o dobro do número de moedas da caixa precedente. Dizem os matemáticos que os números 1, 2, 4, 8 e 16 formam uma progressão geométrica crescente, cuja razão é dois — um sistema binário, portanto. Dada a natureza do problema, é fácil provar que se mantém a mesma progressão fixando os conteúdos das quatro caixas seguintes. Temos então:
6ª caixa: 32 moedas;
7ª caixa: 64 moedas;
8ª caixa: 128 moedas;
E o total de moedas em todas as caixas, portanto, é 255.
— Uassalã!

Pega Matemático!

Ao morrer um pai deixou 90 000 reais aos filhos. São nove homens e cada um deles tem uma irmã. Sabendo-se que a divisão será feita em partes iguais, quanto receberá cada um? Digite a resposta dispondo os algarismos de acordo com os exemplos a seguir: 1 500, 30 000 ou 550 000.

Regra de três e fraçao!

Carla e sua mãe fazem crochê muito bem e resolveram tecer uma colcha juntas. Sabendo que Carla teceria a colcha sozinha em 30 dias e sua mãe, também sozinha, em 20 dias, em quantos dias as duas juntas concluiriam o serviço?










Acontece que após 5 dias de trabalho, das duas juntas, a mãe de Carla precisou viajar e pediu à filha que concluíse o trabalho. Contando, a partir do dia 1º, em que dia o trabalho foi concluído?

Probleminha de 5ª Série (FRAÇÃO)

Uma torneira enche um tanque em 4 horas e, se este tanque estiver cheio, a quantidade de água que escoa pelo ralo o deixa vazio em 5 horas. Se a torneira estiver aberta, mas a água, ao mesmo tempo, saindo pelo ralo, o tanque ficará cheio? Por que? Quanto tempo leverá para encher o tanque?



Será que todo mundo encontrou 20 horas.
Veja porque:
um quarto de um quinto é igual a um vinte avos
1/4 x 1/5 = 1/20
para tornar o tanque com fração inteira ficaria 20/20 portanto em 20 horas o tanque encheria.



Próxima semana outra explicação para o mesmo problema!

Planificação geométrica

Na figura acima, temos a planificação de um cubo:

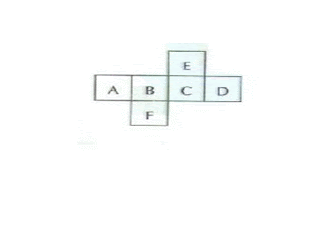
Imagine que o cubo tenha sido montado.
Nesse caso, a face oposta à face B é a face:
a) A
b) C
c) D
d) F

Esta é fácil. Chama-se planificação de figuras geométricas e uma ótima abstração. A resposta certa é a letra c o "D" está atrás do "B" quando você fechar o cubo

Probabilidade!!!!!!

Uma urna possui 6 bolas azuis, 10 bolas vermelhas e 4 bolas amarelas. Tirando-se uma bola com reposição, calcule a probabilidade de sair uma bola azul. (Lembre-se probabilidade é dada em porcentagem.)


Respota:


Resolução:
a. sair bola azul P(A)=6/20=3/10=0,30=30% "
b. sair bola vermelha P(A)=10/20=1/2=0,50= 50% "
c. sair bola amarela P(A) = 4/20=1/5 =0,2 =20% "

Essa é fácil - Equação do 2º Grau

Um número somado com o seu quadrado é igual a 90. Que números são esses?

Essa é só aplicar a fórmula de Báskara.
x+x²=90
transformando
x²+x-90=0

delta
1²-4.1.(-90)
1+360
361

x=-1+ou-19 (raiz de 361)/2

x' = -1+19/2 = 18/2 = 9

x"= -1-19/2=-20/2 = -10

Portanto os números são

9 e -10

Lembra disso..................... Função composta!!!!

Fabiano, a fim de reduzir o preço da conta de telefone de sua casa, decidiu fazer um relatório geral, catalogando a quantidade de ligações feitas por dia juntamente com as suas respectivas tarifas. Nas suas anotações, ele constatou que cada pessoa faz, em média, 4 ligações por dia e também que cada ligação custa mais ou menos R$ 0,70. Com intuito de ajudar Fabiano, vamos analisar matematicamente essa situação:

Se Fabiano não quiser que o valor da sua conta de telefone mensal seja maior que R$ 168, 00, quantas pessoas no máximo deverão utilizar o telefone diariamente?


Resolução:
y = 4x
z = 0,70y
Substituindo 4x no lugar de y na função z:
z = 0,70.4x
z = 2,8x


Se Fabiano não quiser que o valor da sua conta de telefone mensal seja maior que R$ 168, 00, quantas pessoas no máximo deverão utilizar o telefone diariamente?

z = 2,8x
168 = 2,8x
x = 60
60 pessoas durante o mês.

Adotando que o mês tem 30 dias, podemos concluir que o máximo de pessoas que devem utilizar o telefone diariamente, para que não ultrapasse o valor estabelecido por Fabiano, são duas pessoas.

Resposta: 2 pessoas


Com os conceitos apresentados, dadas duas funções reais: f(x) = 2x – 1 e g(x) = x + 2, podemos calcular a função composta de g e f, expressa pela notação (g o f) (x), que é equivalente à g (f(x)). Para isso, devemos substituir no lugar de x na função g a lei de função f.

g(x) = x + 2
g(f(x)) = g(2x – 1) = 2x – 1 + 2 = 2x +1
g(f(x)) ou (g o f) (x) = 2x +1

De modo análogo, podemos calcular a função composta de f em g, substituindo no lugar de x na função f a lei de função g:

f(x) = 2x - 1
f(g(x)) = f(x + 2) = 2.(x + 2) – 1 = 2x + 4 – 1 = 2x + 3
f(g(x)) ou (f o g) (x) = 2x + 3

Praticando...

1) Sendo f(x) = x +2 e f(g(x)) = 5x -1, determine g(x).

f(x) = x + 2
f(g(x)) = g(x) + 2 = 5x – 1
g(x) = 5x – 1 – 2
g(x) = 5x -3

2) Sendo g(x) = x + 1 e f(g(x)) = 4x -5, determine f(x).

g(x) = z
x +1 = z
x = z – 1

f(z) = 4.(z – 1) - 5
f(z) = 4z – 4 – 5
f(z) = 4z – 9 = f(x) = 4x - 9

Palitinho... esse é meu forte!

Uma criança está brincando de fazer quadrados com palitos de fósforos como mostra o desenho a seguir.









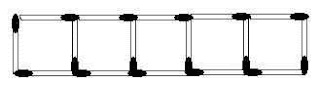
a) Quantos palitos são necessários para fazer 100 quadrados?

b) Quantos quadrados ela fez com 250 palitos?


Para facilitar: essa é uma PA com razão 3
a) Para fazer um quadrado é necessário 4 palitos. Para fazer dois quadrados é necessário 7 palitos. Para fazer três quadrados é necessário 10 palitos , e assim por diante. Então, temos uma progressão aritmética: PA (4 , 7 , 10 , 13 , 16 , ... ), onde o primeiro termo a1 = 4, a razão r = 3 . Assim, temos que encontrar o centésimo termo a100 = a1 + 99r = 4 + 99(3) = 4 + 297 = 301 .
b) O enésimo termo an = a1 + (n-1)r é o número de palitos e o número de termos n é o número de quadrados . Assim, 250 = a1 + (n-1)r. Segue que 250 = 4 + (n - 1)(3). O que implica em, 250 = 4 + 3n - 3. Daí, vem que:: n = (250 - 1) / 3. Logo: n = 249 / 3 = 83 quadrados.

Futebol e Matemática!!!!!

Se num campeonato de futebol é verdade que “quem não faz, leva”, ou seja, time que não marca gol numa partida sofre ao menos um gol nessa mesma partida, então:

a) em todos os jogos os dois times marcam gols
b) nenhum jogo termina empatado
c) o vencedor sempre faz um gol a mais que o vencido
d) nenhum jogo termina 0 x 0, ou seja, sem gols
e) resultados como 1 x 0, 2 x 0 ou 3 x 0 não são possíveis


Essa foi muito fácil - Letra certa d - alguém vai ter que marcar, pois quem não faz, leva, ou ele ganha ou ele perde. Isso só acontece na Matemática.

Probleminha simples de 6ª série...

A mãe pede ao filho Antoninho:
- Filho vai no Empório ( nome de casas comerciais) do seu Joaquim e compra manteiga.
O filho bem depressa vai ao Empório. Chegando lá ele pede ao seu Joaquim.
- Seu Joaquim, seu Joaquim eu quero manteiga. O Senhor tem aí?
- Tenho sim Antoninho, responde o seu Joaquim, mas só tenho 1 milésimo de tonelada.
- Ah seu Joaquim, mas eu só quero 1 hectograma da manteiga.

Pergunta:
Quanto de manteiga tem o Seu Joaquim pra vender?

Quanto de manteiga comprou o Antoninho?

Fácil , fácil!!!!!!




Fácil Mesmo!!!!!!!!!!!!!!!!!!

O seu joaquim tem 1kg de manteiga - 1 milésimo da tonelada 1.000kg dividido por mil.

O Antoninho 100 g de manteiga.

Divisão é fácil; o difícil é problema com divisão....

Numa divisão entre numeros naturais, o quociente é o igual ao divisor, e o resto é o maior possivel. Se o resto for igual a 11, qual será o dividendo ?

Resposta:

Como o resto é 11 e ele é o maior possível, assim o divisor só pode ser 12 e o quociente também. Então fica assim: 12 x 12 = 144 + 11 (que é o resto) = 155 é o dividendo.

Um abraço!!!!